Chapter 2

Overview

The concept of Function is central to the study of mathematics. If you do not gain a good understanding of functions your future math classes will be extremely difficult.

I will give a couple of informal ways to think about a function below and then give a formal definition.

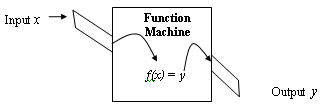
1. A way of thinking about a function is a “function machine” (often called a function box or black box).
   
   So, given a function machine (a function) we must first give it an Input to “operate” on. We will name this input “x”. Then the function (machine) “operates” on “x” and gives us an output “y”.

2. Another way to think about a function, f, is as a Mapping from a first set, D, to a second set, R.

   

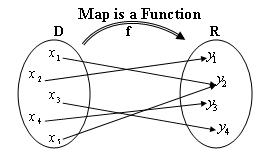
   Note that each x in D gets “Mapped” to one and only one y in R! This is the most important aspect of a function.

   Notice that it is OK for two different x’s to get mapped to a singe y.
   Therefore the following mapping is NOT a Function since a single x, namely x₂, gets mapped to two different y’s, namely y₁ and y₃.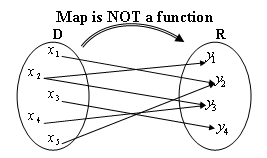

   

   In the first diagram no matter what x I am I know exactly which y to go to, and it is OK for some other x to meet me there!

   BUT, in the second diagram if I am x₂ I am confused since I can’t decide which y to go to, y₁ or y₃! (Thus this is not a function!)

   This gives us an easy way to think about which mappings are functions and which mapping are NOT functions.

3. The Definition of a Function (from the text).

   A Function from a set D to a set R is a correspondence or rule (or mapping) that assigns to each element x in D exactly one element y in R.

   The set D is called the “Domain” of the function and the elements x of D are the “input values”.
   
   The elements y of R that correspond to the input values are the “output values”. The set of all possible output values is called the “Range” of the function.

   It is important that we understand the concept of function. To start down the road of understanding you should convince yourself that each of these three descriptions of a function are fundamentally exactly the same!

   For example, go through each description and make sure you understand and can describe in words the Domain and the Range.