   |
| Welcome | Getting Started | Resources | Site Map | Chapter 1 | 2 | 4 |
Chapter 4
4.1 – Exponential Functions |
 |
 |
Objectives
- Know the graph and properties of
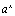and 
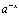for base a > 1. - Use the graph of 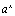to sketch related graphs of the form
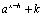. - Perform calculator evaluations of 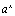for various bases and
exponents.
- Use the natural exponential function
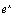in graphing and application
problems.
Examples/Definitions
Exponential Function: The function 
is called the exponential
function with base a.
The key properties of the function with a >1 are:
- Domain of 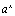is the set of all real numbers x.
- Range of 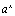is the set of all positive real
numbers x.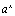
- is one-to-one and
is an increasing function.
- The graph of 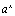has y = 0 (the x-axis) as a horizontal
asymptote.
One-to-one Property
If 
then x = y.
Algebraic Properties of Exponential Functions
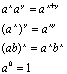
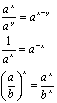
Formula for compound interest
where
P is interest, B is the balance, I is interest rate per interest period, n is
the number of compounding periods and t is the number of years.
When interest is compounded continuously, we use the formula:
| Welcome | Getting Started | Resources | Site Map | Chapter 1 | 2 | 4 |
|
