 |
| Welcome | Getting Started | Resources | Site Map | Chapter 1 | 2 | 4 |
Chapter 4
4.2 – Logarithmic Functions |
Objectives
- Understand logarithmic functions are the inverse functions of exponential functions.
- Know the graph of
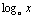 and how it relates to the graph of
and how it relates to the graph of 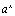 .
. - Use properties to express exponential equations in logarithmic form and logarithmic functions in exponential form.
- Use curve sketching methods to sketch graphs related to
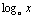 .
. - Perform calculator evaluations of
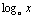 for various bases a and
positive values of x.
for various bases a and
positive values of x.
Examples/Definitions
Logarithm with base a: The inverse function of the
exponential function ![]() is
denoted by
is
denoted by ![]() and
is called a logarithmic function.
and
is called a logarithmic function.
Natural Logarithm: The inverse function of the natural
exponential function ![]() is
denoted by
is
denoted by ![]() and
is called the natural logarithm.
and
is called the natural logarithm.
The key properties of ![]() for base a > 1 are:
for base a > 1 are:
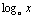 has
the domain
has
the domain 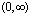
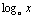 has
the range
has
the range 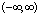
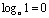 for
any base a
for
any base a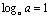 for
any base a
for
any base a- the graph of
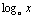 has the vertical asymptote x = 0 (y-axis)
has the vertical asymptote x = 0 (y-axis)
The same properties can be extended to the natural logarithm function:
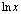 has
the domain
has
the domain 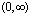
 has
the range
has
the range 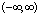
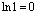 for
any base a
for
any base a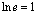 for
any base a
for
any base a- the graph of
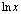 has the vertical asymptote x = 0 (y-axis)
has the vertical asymptote x = 0 (y-axis)
Inverse Properties
![]() for
all positive real numbers x
for
all positive real numbers x
![]() for
all real numbers x
for
all real numbers x
The inverse properties also hold for the natural logarithmic function:
![]() for
all positive real numbers x
for
all positive real numbers x
![]() for
all real numbers x
for
all real numbers x
| Welcome | Getting Started | Resources | Site Map | Chapter 1 | 2 | 4 |