Week 1

1.5 - Techniques for Solving Equations

Objectives

1. Find the solutions & solution sets of equations.
2. Solve linear equations using algebraic techniques.
3. Understand the x-intercept of a given equation y = u, relates to the solutions of the equation u = 0
4. Approximate solutions of an equation by using a graphing calculator.
5. Determine if two equations are equivalent.
6. Solve quadratic equations by factoring, completing the square and using the quadratic formula.
7. Solve equations with fractional or radical terms both algebraically and graphically.
8. Solve polynomial equations by factoring or graphing.
9. Determine the number of solutions of an equation of the form .

Examples/Coaching Tips

The following definitions are used in this section:

• A solution to an equation is a value of the variable that makes the equation true.
• The collection of all solutions to an equation is called the solution set.
• Two equations are equivalent if they have the same solution set.

Example 1

Determine if the following equations are equivalent:

3 + x = 7 and 5x +2 = 22

Determine the solution set for each equation:

3 + x = 7

x = 4 is the only solution for the equation

5x + 2 = 22

5x = 20

x = 4 is also the only solution for the given equation, so the equations

3 + x = 7 and 5x + 2 = 22 are equivalent.

Example 2

Solve the equation

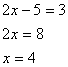
Note: An equation is linear if it can be put in the form

where a, b, and c are constants with . The graph of a linear equation is a line.

Quadratic Equations

Note: A quadratic equation of the form , when b = 0, can be solved by taking square roots.

Example 3

Solve

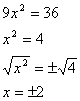
So the equations has two solutions

Example 4

Solve by completing the square,

First get all constants on one side of the equation:

We must add the term or 9 to both sides of the equation:

We can now factor the left side of the equation:

Taking the square root of both sides, we have

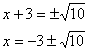
We have two solutions to the equation.

Quadratic Formula

When a quadratic doesn’t factor easily and the coefficient of x is non-zero, the quadratic formula may be used. The quadratic formula is used for quadratics of the form and the solutions are:

The quadratic formula can help us determine the number of solutions an equation has by using the discriminant, .

When there is 1 real solution

When there are no real solutions

When there are 2 real solutions.

Rational & Radical Equations

The following are examples of the steps used when solving equations involving rational and radical expressions.

Example 5

Solve

To solve the equation, we must first multiply both sides by the Least Common Denominator:

This leaves:

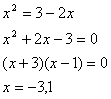
, when substituting this value into the original equation, it gives an undefined value.

The only solution is x = -3

Example 6

Solve

We will start by squaring both sides of the equation to eliminate the radicals:

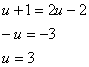
With equations involving radicals, we must check our solution by plugging it into the original equation and it is a solution.

Polynomial Equations

Polynomials are sums & differences of constants multiplied by positive integer powers of a variable.

The degree of a polynomial is the largest exponent that occurs in the polynomial. A solution to a polynomial equation is called a zero or root.

When finding solutions of an equation, we use the property:

ab=0 if and only if a=0 or b=0

Example 7

Solve the polynomial equation

First get the equation in standard form:

We can now solve the equation by factoring:

Either or , so x = 1, 7 are the solutions.

When solving equations in the form , we must take a root of both sides.

If n is even, the equation will have 2 solutions:

If n is odd, the equation will have only 1 solution:

Note: There are 2 ways to express the solution,

Example 8

Solve the equation

First we will put into the form:

We will next take the 3 rd root of both sides. Since our exponent is odd, there should only be one solution.

If the exponent was even, we would have 2 solutions to the equation.