Chapter 1

1.6 – Inequalities

Objectives

1. Solve linear inequalities and express the solution set in inequality notation, set builder & interval notation.
2. Graph the solution set of an inequality on a number line.
3. Solve equations & inequalities involving absolute value terms using algebraic & graphical techniques.
4. Solve  inequalities involving polynomials algebraically and graphically.
5. Understand the idea of absolute value and how it relates to the distance from a point to zero on the number line.

Examples

We have learned ways to solve equations, now we will look at different types of inequalities. 

Linear Inequalities

An inequality is linear if it can be put in one of the following forms:

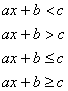
Example 1

Solve the inequality 

The solution is the set of all real numbers x with .  The solution can be expressed in interval notation as 

  Absolute Value Equations & Inequalities

  An absolute value sign is removed if , then

 if and only if   u = c  or u = -c

Note:  u can be any expression involving real numbers & variables

Example 2

Solve the equation

Solution

The equation  is equivalent to the pair of equations   and  , which have the corresponding solutions,   and   Thus, the equation  has two solutions,

Example 3

Solve the inequality  .

Rewrite the inequality as two inequalities:

2x – 3 > 5            or            2x – 3 < -5

We now can solve each inequality:

2x  >  8                                2x < -2

x > 4                                      x < -1

Writing the solution in interval notation we have:

Polynomial Inequalities

We solve polynomial inequalities with the help of a graph.  We use the fact that any polynomial is always positive or always negative between consecutive zeros.  To solve an inequality graphically, the steps are given in the text.