Chapter 1

1.7 Lines

Overview

Objectives

1. Know the definition of the slope of a line.
2. Understand slope of a line as a rate of change.
3. Know the tests of slopes of parallel and perpendicular lines.
4. Find the slope of a line given two points or one point and slope of the line.
5. Understand linear interpolation and linear extrapolation.

Examples and Definitions

Note: Slope is defined as or the change in y divided by the change in x.

Given two points , the slope of the line containing these two points is given by:

There are two forms of the equation of a line:

Slope-intercept equation:

where m=slope and b=y-intercept

Point-slope equation:

where m=slope and is a known point on the line

Example

A line passes through the points (2, -3) and (5, 9). Find the equation of the line and the slope of a line perpendicular to the line.

The line has slope

Since (2, -3) is a known point on the line and m=4, we can use point-slope equation of the line:

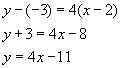
This gives the equation of the line in slope-intercept form.

Given the slope of a given line = m, the slope of the line perpendicular = -1/m

So, the slope of the perpendicular line =

Linear interpolation and extrapolation

In this section, the ideas of linear interpolation and extrapolation are explained. These ideas are used when given data lies roughly on a straight line. Predictions are made based on the data using a straight line to model what will happen at points where no data exists.