Chapter 1
Review - Equations and Inequalities
|
 |
 |
This review is basically a check-off list of the important concepts and
processes from chapter 2 along with some reminders of the most common misconceptions.
Section 1.4 ~ Graphs of Equations
- Determine if a given point lies on the graph of a given equation.
- Sketch the graphs of functions given in symbolic form and as a table of values.
- Determine the center and radius of a given circle in symbolic form. This will often require “completing the square”.
- Determine the symbolic equation of a circle which has the given attributes.
- Match symbolic equations with their corresponding graphs.
- Choose an appropriate “window” on your calculator to view the graph of a particular function.
Hints
- Remember to put the equation of a circle in standard form
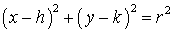 before determining the center. A common mistake is to say that before determining the center. A common mistake is to say that 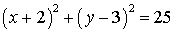 has center has center 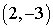 and radius 5. But when put in standard form and radius 5. But when put in standard form 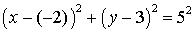 we see that the center is we see that the center is 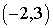 and the radius is 5! and the radius is 5!
Section 1.5 ~ Techniques for Solving Equations
- Understand the meaning of the terms “solution”, “solution set”, and “equivalent”, with respect to equations and inequalities.
- Know how to find the solution set of equations to determine if two equations are equivalent.
- Know the “properties of equations”
- Know how to approximate the solutions of an equation graphically.
- Know the different forms of a linear equation: standard, slope-intercept, and point-slope.
- Know how to state the solution set of an inequality using “interval notation”, “set builder notation”, and the “number line”.
- A Rational equation is any equation that contains a rational expression. A rational expression is the ratio of two polynomials.
- Understand and know how to use the definition of absolute value (find the definition in the chapter 2 overview.)
- Determine the solution set of equations involving absolute values.
- Translate a verbal statement into a mathematical statement involving absolute value.
- Determine the solution set for equations involving absolute value.
- By definition a quadratic equation is any equation that can be put in the form
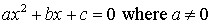 , which is called the standard form of a quadratic equation. Notice that this is a special case of a polynomial, a polynomial of degree 2. Also note that if we let , which is called the standard form of a quadratic equation. Notice that this is a special case of a polynomial, a polynomial of degree 2. Also note that if we let 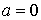 we would no longer have a quadratic equation but just a linear equation. we would no longer have a quadratic equation but just a linear equation.
- Know how to solve quadratic equations by: 1) factoring, 2) completing the square, and 3) via the Quadratic Formula (see the chapter 2 overview.)
- Know what the “Discriminant” of the Quadratic Formula is, what it tells us about the zeros of a quadratic equation, and how it works.
- Know how to recognize “equations of quadratic type” and how to use quadratic methods to solve them.
- Translate verbal statements into mathematical statements.
- By definition a polynomial equation is any equation that can be put in the form
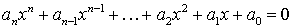 , which is called the standard form of a polynomial equation. , which is called the standard form of a polynomial equation.
- Know the “Zero- Product Property” and its significance in solving equations.
- Know how to solve polynomial equations by: 1) factoring, and 2) applying the
 to the entirety of both sides of equations of the form to the entirety of both sides of equations of the form 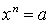 . .
- Determine the solution set for radical equations. (The first step in doing this is to clear the equation of its fractions by multiplying each term of the equation by the least common multiple of all the denominators of the equation.)
- Determine the solution set for Radical equations, equations containing a root(s).
- Understand why we must check all solutions of rational and radical equations to determine if they are TRUE solutions.
Hints
- When using the multiplication or division properties, be sure you are not multiplying or dividing by an expression that could be zero.
- The first step in solving equations that involve absolute value is to write the equivalent equation(s) without the absolute value.
- “OR” goes with Union and “AND” goes with Intersection.
- Think of “
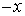 ” as the “opposite of ” as the “opposite of 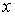 ” and NOT “negative ” and NOT “negative 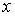 ”. ”.
- To use the “Zero-Product Property” in solving an equation one side of the equality must be Zero!
Section 1.6 ~ Inequalities
- Know how to use the “properties of equations” to create a sequence of equivalent equations to determine the solution sets of linear inequalities.
- Know what is meant by “compound” inequalities, how to solve them.
- Know how to use the set operations “ Union,
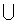 “and “Intersection, “and “Intersection, 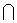 ”. ”.
- Know the different types of compound inequalities and which type corresponds to the words “AND” and “OR” as well as to the set operations “ Union,
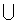 “and “Intersection, “and “Intersection, 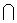 ”. ”.
- Know how to solve polynomial inequalities: 1) via a table, and 2) graphically.
Hint
- When solving inequalities we use the same “properties” that we use for solving equations with the exception that when we multiply or divide by a negative number we must switch the direction of the inequality symbol.
Section 1.7 ~ Lines
- Be able to compute the slope of a line given various types of information.
- Know and be able to use the three forms of an equation of a line:
- Point-Slope Form
- Slope-Intercept Form
- Standard Form
- Be able to find the equation of a line given particular attributes about the line.
- Know the relationship between the slopes of Parallel and Perpendicular lines.
|

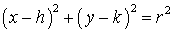 before determining the center. A common mistake is to say that
before determining the center. A common mistake is to say that 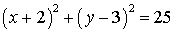 has center
has center 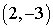 and radius 5. But when put in standard form
and radius 5. But when put in standard form 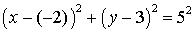 we see that the center is
we see that the center is 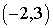 and the radius is 5!
and the radius is 5! 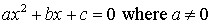 , which is called the standard form of a quadratic equation. Notice that this is a special case of a polynomial, a polynomial of degree 2. Also note that if we let
, which is called the standard form of a quadratic equation. Notice that this is a special case of a polynomial, a polynomial of degree 2. Also note that if we let 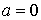 we would no longer have a quadratic equation but just a linear equation.
we would no longer have a quadratic equation but just a linear equation. 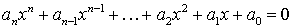 , which is called the standard form of a polynomial equation.
, which is called the standard form of a polynomial equation.  to the entirety of both sides of equations of the form
to the entirety of both sides of equations of the form 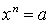 .
. 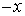 ” as the “opposite of
” as the “opposite of 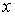 ” and NOT “negative
” and NOT “negative 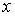 ”.
”. 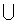 “and “Intersection,
“and “Intersection, 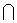 ”.
”. 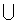 “and “Intersection,
“and “Intersection,  ”.
”.