Chapter 2

2.2 Graphs & Functions

Overview and Examples

Objectives

1. Find the zeros of a function both graphically and algebraically.
2. Given the graph of 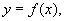sketch the graph of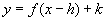
3. Define the terms relative minimum or maximum, global minimum or maximum, and the phrases “increasing on the interval” & “decreasing on the interval”.
4. Use the graph of a function to determine minimum and maximum values.
5. Use the graph of a function to determine intervals where the graph is increasing or decreasing.

Examples and Definitions

The graph of an even function is symmetric with respect to the y-axis.

The graph of an odd function is symmetric with respect to the origin.

Given the graph of > the graph of is a shift of the graph h units horizontally and k units vertically.

Example 1

Given the graph of the parabola , which is a parabola opening upward with vertex (0, 0). Explain how to sketch the graph of .

First we will rewrite the function in the form:

The graph of this function is a translation of the graph of , 2 units to the left and 3 units up. The vertex of this parabola is (-2, 3).

Example 2

Show that the function is odd.

If a function is odd,

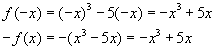
Since the function is odd and its graph is symmetric about the origin.

Note: If a function is even, and its graph is symmetric about the y-axis.