Chapter 2

2.3 Combinations of Functions

Overview & Examples

1. Understand how the functions and 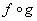are defined.
2. Evaluate the different combinations of functions for different choices of f and g.

Sums, differences, products and quotients of functions

The following symbols and definitions are used to express the sums, differences, products and quotients of functions:

Sum:

Difference:

Product:

Quotient:

Example 1

Find the sum, difference, product and quotient of the functions and .

Solution

Sum: for all

Difference: for all

Product: for all

Quotient: for all except x = 3

Composition of Functions

If f(x ) and g(x) are given functions, then the function that assigns the input x and the output f(g(x)) is called the composition of f and g. The notation for the composition will normally be expressed as or

Example 2

Find the compositions , and if and .

for

for

Since g(4)=0, then