Chapter 2

2.4 Inverses of Functions

Overview & Examples

Objectives

1. Understand the idea of an inverse function.
2. Apply the horizontal line test and understand how it relates to a one-to-one function.
3. Know the geometric and algebraic tests to determine if a function has an inverse.
4. Find the domain and range of an inverse function, given the domain and range of the original function.
5. If a given function has an inverse, sketch the graph of the inverse function.

Examples/Definitions

Inverse functions are functions that reverse each others operations. Two functions are inverses if the following is true:

A function f has the property that there is a function g such that

for all x in the domain of f

for all x in the domain of g

then g is called the inverse function of f and g is usually denoted by (which means “f inverse).

Example 1

Find the inverse function of, if it exists.

Solution

First replace f(x) with x and replace x with y

Now, solve for y

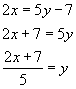
The function we have found is the inverse of f(x), so we will replace y with the inverse notation

Some facts about inverse functions:

• Not all functions have inverses.
• Domains and ranges trade places for inverse functions.
• An inverse function does not mean one divided by the function.
• A function has an inverse if and only if every horizontal line meets the graph of the function at only one point. This is called the horizontal line test and a function with this property is called one-to-one.
• A function has an inverse if and only if it is one-to-one.
• If f has an inverse function, then the graph of the inverse function can be found by reflecting the graph of f across the line y = x.

Example 2

Determine if the function has an inverse.

Solution

For a function to have an inverse, it must pass the horizontal line test . By graphing f(x), one can see it is a parabola and does not pass the horizontal line test and does not have an inverse.