Chapter 2

2.5 Selected Functions

Overview & Examples

Objectives

1. Find the vertex of a parabola by completing the square.
2. Sketch the graph of a parabola .
3. Find the minimum or maximum value of a quadratic by finding the vertex of the parabola.

Examples/Definitions -- Linear & Quadratic Functions

A function is linear if it can be expressed in the form . The graph of is a line.

A function is quadratic if it can be expressed in the form , where , b, and c are given numbers. The graph of f is a parabola that opens upward if a is positive and opens downward if a is negative and has a vertex at the point .

You can also find the vertex by completing the square.

Example

Complete the square to find the graph of the quadratic function .

Solution: To complete the square the term must have a coefficient of 1, so first we must factor out 3 from any terms containing the variable x.

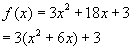
To complete the square we must add and subtract the same constant, so we are not changing our original function just writing it in a different form. We must also remember there is a 3 multiplied by everything in parentheses, so we will be multiplying the term we add by 3.

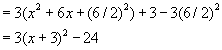
By using the translation properties we learned in an earlier lesson, the graph of this function is a translation of the function by 3 units to the left and 24 units down. So the graph of this function is a parabola that opens upward and has a vertex at the point (-3, -24). This vertex also gives the location of the minimum function value for .

Piecewise functions

Piecewise functions are functions whose outputs are defined in more than one part.

Example

Evaluate the following piecewise function f at ,4

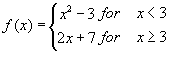
Since x = -1 and x = 0 satisfy x < 3, we will evaluate f using the first line in the formula:

Since x = 3 and x = 4 satisfy , we will evaluate f using the second line in the formula: