Chapter 2

2.6 Modeling with Functions & Variation

Overview & Examples

Objectives

1. Know the meaning of directly proportional, inversely proportional, jointly proportional, and proportionality constant.
2. Find the proportionality constant from the given data.
3. Understand the idea behind best least-squares approximation.

Examples/Definitions - Variation

Example

If z varies inversely as x, and z = 4 when x = 8, find z when x = 2.

Solution

Since z varies inversely as x, then this is an inverse variation problem of the form:

where k is the proportionality constant.

We can use the information given in the problem to first solve for k:

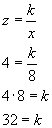
We will now use this value for k to solve for z when x = 2:

These same steps will be used for many variation problems, by first solving for k and using this value to solve for some unknown variable.

Best Least-Squares Fit

Given data points may not always lie on a straight line, but there is a way determine a “best” fitting line for the data. The “best” fitting line is one that keeps the sum of the squares of the distances between each data point and the line at a minimum. This line is called the best least-squares fit to the data. Most calculators have a least squares data fitting program. You input the data points and the calculator determines the best least-squares fit by giving you coefficients a and b for the equation .

If the data does not appear to lie anywhere close to a straight line there may be a different model that fits better such as exponential, logarithmic, or quadratic. Most calculators will have these models built in as well.