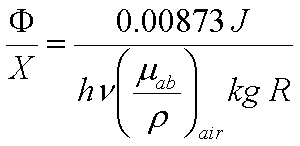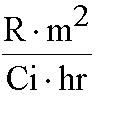Topic 5 - Dose Units
Kerma |
 |
 |
- “Sum of the initial kinetic energies per unit mass of all charged
particles produced by the radiation”
- This is regardless of where the energy is deposited
- Bremsstrahlung photons are not counted, whether they escape or
not
- Annihilation radiation is not counted, regardless of fate of
annihilation photons
- Initial positron, if primary ionizing particle, is counted
Energy Transfer - A Two Stage Process - Kerma and Absorbed Dose

Correction/Clarification on Kerma
- Etr is just the kinetic energy received by charged particles
in a specified volume V, regardless of where or how they spend the
energy
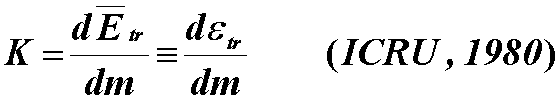
- Kerma is the expectation value of the energy transferred to charged
particles per unit mass at a point of interest, including radiative-loss
energy, but excluding energy passed from one charged particle
to another
Quantities to Describe a Radiation Beam
- Fluence
- Energy fluence
- Energy / area
- Y = dN hn/da
- Fluence rate
- # photons/(time area)
- f = dF/dt
- Energy fluence rate
- Energy / (time area)
- y= dY/dt
Relationship of Kerma to Photon Fluence

• > is attenuation coefficient
• is density
-

- gives the number of photon interactions that take place per unit
mass of material.
- m is attenuation coefficient
- r is density
- For a spectrum of energies that can be described by dΦ(hv) /d
hv, then:
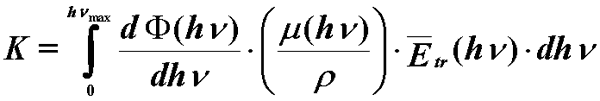
Calculating Kerma
- Given incident on a block of carbon
- 10 MeV photons
- F = 1014 m-2
- What is kerma?
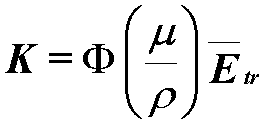
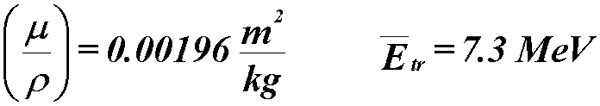
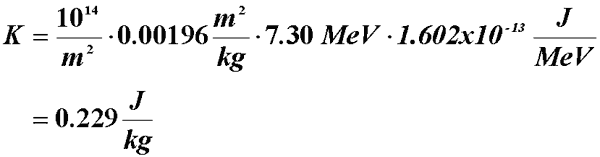
- Kerma is easy to calculate - but very difficult to measure!
Relating Kerma & Absorbed Dose
- Kerma
- a measure of kinetic energy transferred at a point in space.
- Absorbed dose is more “interesting”.
- Energy is transferred in the medium
- not all is retained there.
- absorbed dose is the energy retained in the medium brought about
by the ionizations along the track of the charged
particle.
- Kerma and Absorbed Dose do not take place at the same location
Calculating Absorbed Dose

- dEab is the mean energy “imparted” by the ionizing radiation
into a mass, dm.
- Mass should be sufficiently small so that it the absorbed dose
is defined at a point, but not so small that statistical fluctuations
become important
- From the previous example, dEtr = 7.3 MeV
- fraction of 10 MeV photon energy transferred to the medium.
- A smaller amount is absorbed along the electron track: dEab
= 7.06MeV
- dEtr- dEab
- The difference, 7.30-7.06 = 0.24 MeV, is bremsstrahlung.
- What is the path length of the 7.3 MeV electron in C?
- Estimate from graphs or tables of electron ranges,
- ~ 4.2 g cm-2.
- Divide by the density of carbon
- Path length: 1.9 cm.
Dose and Kerma

Important Relationship
- Relate absorbed dose in air to exposure:
- assuming CPE (electronic equilibrium)
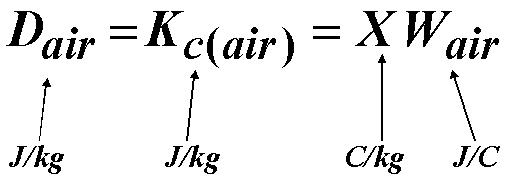
Electronic (Charged-Particle) Equilibrium
- The transfer of energy (kerma) occurs upstream from the absorbed
dose.
- Kerma can be easily calculated from fluence
- Absorbed dose cannot. Why?
- Kerma remains constant
- Absorbed takes time to build up as upstream electrons increase:
No Attenuation of Photon Beam, Φ Constant

-
 Number of electron tracks set in motion by photon interaction
Number of electron tracks set in motion by photon interaction
- Φ constant with depth (small # interactions)
- Same # electrons set in motion in each square
- i.e., interactions per volume constant through target
Absorbed Dose and Kerma

Beam Unattenuated
- Same number of photon tracks set in motion in each square
- e.g., square D is traversed by 400 tracks
- ionization in D is the same as total ionization started in A
- absorbed dose is proportional to ionization produced in each
saure
- dose reaches a maximum at R (range of 2o)
- kerma constant with depth, equals absorbed dose beyond R
Absorbed Dose and Kerma

Attenuation of Photon Beam
- Beam attenuation,
- Φ decreases with depth.
- Dose increases to a maximum (at maximum range of particle) overshoots
then tracks kerma.
Attenuation of Photons in Tissue
| Isotope |
Maximum Dose Septh (mm in Tissue) |
Beam Attenuation (% of original beam) |
| 137Cs |
2 |
1 |
| 60Co |
5 |
2 |
| 6 MV |
15 |
6 |
- CPE will generally exist in a uniform medium at a point more than
the maximum range for the secondary charged particles from the boundary
of the medium
Relating Energy Fluence and Exposure

- Radioactive beam incident on an area
- What is relationship between energy fluence and exposure at
point p?
- Assume small mass of air at p
-
The dose at p is: D= F(m/r)Eab= Y (mab/r)
- Can relate to R as:
- 1 R = 0.00873 J/kg, then
-
Y/X = 0.00873 J/ ((mab/r)kg R)
- Complicated variation of energy absorption coefficient for
air and energy of beam
Relating photon fluence to exposure
- Relationship between energy fluence and photon fluence:
- F = dN/da
- Y= dN hn/da
- So, Y= F hn, and
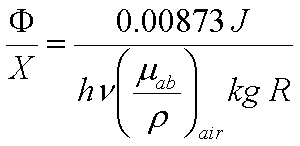
Specific Gamma Ray Emission
- G = Specific Gamma Ray Constant
- Has been calculated for many gamma ray emitting isotopes
- Can ‘easily’ be calculated
- Where do the numbers come from?
Specific Gamma Ray Constant
- Assumes that the absorption of photons in air is constant over a
large range
- See Figure 5.18 in text (p. 148) or Table 5.3 (p. 149)
- Absorption is almost constant from 60 keV to almost 2 MeV
- Assumes photons isotropic, no ‘buildup’
- Eliminates many constants for ease of calculation
- 3.5 ´ 10-3 m-1 linear absorption coefficient
- Combine terms

- Thus, 0.5 is the value of all of the constants combined
- Equation 6.18 can then be written
- G = 0.5 S fi ´ Ei
- Remember this is only useful for photons
- Some values are listed on page 187

|


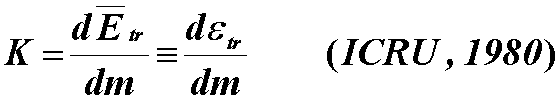


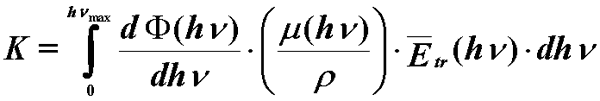
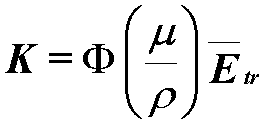
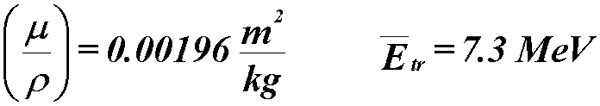
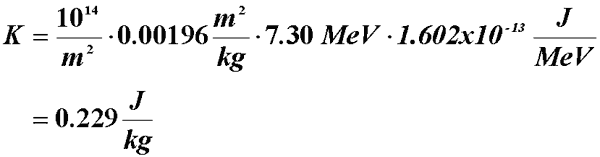


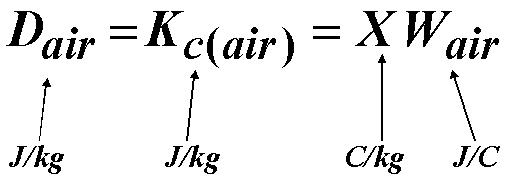

 Number of electron tracks set in motion by photon interaction
Number of electron tracks set in motion by photon interaction