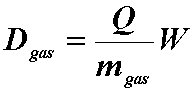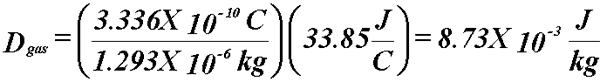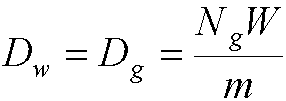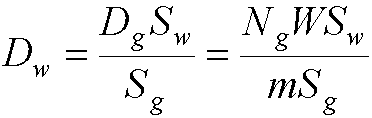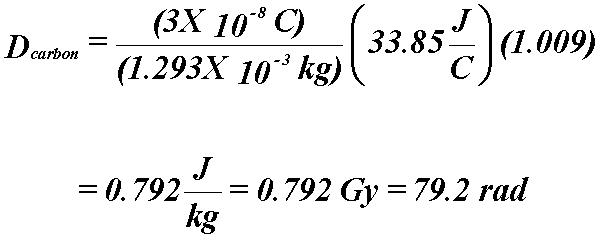Topic 5 - Dose Units

Radiation Dosimetry

Dosimetry Overview

Units
Specific Gamma-Ray Emission
Beta Radiation
Internally Deposited Radionuclides
Neutrons

Introduction

Dosimetry attempts to quantitatively relate specific radiation measurements to chemical/biological changes that could be produced
Essential for quantifying biological changes as a function of radiation received
For comparing experiments
For other purposes
Radiation interaction
- Produces ionized and excited atoms and molecules
- Secondary electrons
  - Produce additional ionizations and excitations
  - Finally all energies are expended.
- Initial electronic transitions rapid (<10^-15s⁾
- Represent the initial physical perturbations from which all effects evolve.
So, ionization and energy absorption are the starting point for radiation dosimetry

Quantities and Units

Absorbed Dose
- Primary physical standard in dosimetry
- Defined as energy absorbed per unit mass from any kind of ionizing radiation in any target.
SI Unit of absorbed dose,
- Called the gray (Gy)
- 1 Gy = 1 J kg^-1
Historical (older) term
- rad, (100 erg g^-1)
1 Gy = 10⁷ erg/10³g = 10⁴ erg/g = 100 rad
Exposure
- Defined for X and gamma radiation
  - In terms of ionization of air
  - Old unit called “roentgen” (R)
  - Initially defined in 1928, current definition is:
  - 1 R º 2.58 x 10^-4C kg^-1 of air, exactly
- Applies only to electromagnetic radiation; the charge and mass refer only to air.

Roentgen - original definition

Amount of radiation that produced 1 esu of charge in 1 cm³ of air at STP
- 1 esu = 3.335 x 10^-10C
- At STP air has a density of 0.001293 g cm^-3
- 1 kg of air has a volume of 7.734 x 10⁵ cm³
1 R = 3.335 x 10^-10C cm^-3of air
How much energy is absorbed in air from 1R?

Absorbed Dose and Exposure

What is the absorbed dose in air when the exposure is 1 R?
- Need to know W for air
  - 33.7 eV/ip = 33.7 J/C.
- 1 R º 2.58 x 10^-4C/kg x 33.7 J/C = 8.8 x 10^-3 J kg^-1
This equals 8.8 x 10^-3 Gy (0.88 rad)
- Similar calculations show that 1R would produce a dose of 9.5 x10^-3 Gy (=0.95 rad) in soft tissue.
  - Why is there a difference between air and tissue???
- This is why one can say that 1 R ~ 1 rad in tissue.

Exposure Measurement - Free Air Chamber

Feasible to measure exposure at radiation energies between few keV and several MeV
Definitive measure is by laboratory device known as free air chamber
X-ray beam enters through a portal and interacts with cylindrical column of air defined by entry diaphragm
Ions created in defined space are measured

Parallel Plate Free-air Ionization Chambers

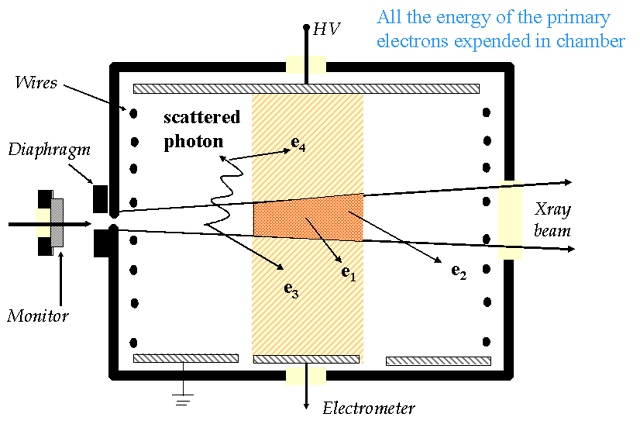
Free Air Chamber

Photons enter chamber and interact with fixed quantity of air
- PE, CS
Ions from air collected by plates
Lead lined (shielded)
Electric fields are kept perpendicular to plates by guard rings and guard wires
- Guard wires assure uniform potential drop across plates
Field intensity is ~ 100 V/cm
Collect ions prior to recombination
Voltage low enough so no secondary ionizations
Current flow is measured
All energy of primary electrons must be deposited in sensitive volume of air for meter to work properly
What if all primary electrons are not collected in sensitive volume?
If equal number coming in from outside of sensitive volume as is going out: Electronic Equilibrium

Electronic Equilibrium

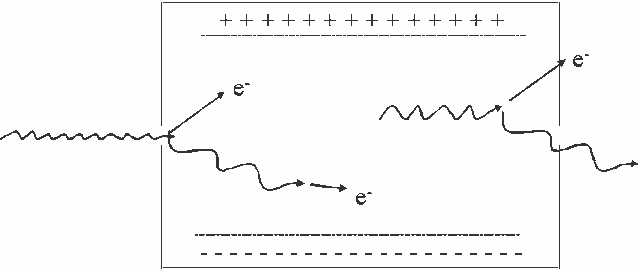
For every electron which escapes the sensitive volume, another electron of equal energy enters the sensitive volume and deposits energy in the detector
A layer of air between entrance port of free air chamber and the sensitive volume can provide enough air so that electronic equilibrium is attained

Free-Air Ionization Chamber

http://physics.nist.gov/Divisions/Div846/Gp2/wafac.html

Wide-Angle Free Air Chamber (WAFAC)

NIST primary standard for low-energy photon-emitting brachytherapy sources such as ¹²⁵I.
- Variable volume, circular free-air chamber,
- Symmetrical about the beam axis, with lines of force parallel to the beam axis.
- 80 mm diam. Tungsten aperture (not visible at right) chamber used to define the beam.
- 3 electrodes: polarizing, middle, and collecting electrode (farthest from the source and left in the picture) about 150 mm in diameter.
- Chamber volume varied from ~75 cm³ to 804 cm³ by changing middle electrode from 11 mm to 152 mm.

Measuring Exposure

Free air chamber practical only as laboratory device
Portable instrument needed

Exposure Measurement: Air Wall Chamber

Practical alternative to free-air chamber
Built as a capacitor
- Central anode, insulated from rest of chamber
- Given an initial charge
- When exposed to photons, 2⁰ electrons neutralize charge & lower potential between anode and wall
- Change in potential difference is proportional to total ionization (and therefore exposure)
Better for field use than the Free Air Chamber
Simulates compressing air into a small volume by using ‘air equivalent’ material
- X-ray absorption properties similar to that of air
Walls must be thick enough to generate enough primary electrons
Walls must be thin enough so that primary radiation is not shielded
Ideal air wall chambers have only primary electrons ionizing the air in the sensitive volume
Ideal wall thickness is almost energy independent over a range from 200 keV to almost 2 MeV (See figure 6.4)
Greater than 3 MeV primary electrons have long range
Impractical to build air wall chamber of sufficient size
- When walls are made thick enough to generate primary electrons, radiation is attenuated significantly
- Radiation intensity will no longer be constant
- Primary electrons not produced uniformly
- No electronic equilibrium

Exposure-Dose Relationship

Exposure
- measures charge produced in a mass of air
- C/kg
Absorbed dose
- Measures energy absorbed per mass
- J/kg
How to relate measurement in air to absorbed dose in something besides air?
Energy absorption in air ¹ energy absorption in tissue
Dose in air ¹ dose in tissue
1 R = 87.7 ergs/g_air = 95 ergs/g_tissue
1 rad = 100 ergs/g_tissue
For regulatory purposes, frequently 1 R is assumed to be equal to 1 rad
Conversion can be done if required

Exposure to Dose Conversion

Equation 6.12
m_m = Energy absorption coefficient for tissue
m_a = Energy absorption coefficient for air
r_m= Tissue density
r_a = Air density

Bragg-Grey Theory

How to measure absorbed dose?
The best way would be calorimetry...but not very practical. Instead, absorbed dose is measured by:
- measuring ionization
- use of correction factors
- calculating (approximating) dose
This is done with BRAGG-GREY CAVITY THEORY

Measurement of Absorbed Dose

Bragg-Gray principle relates ionization measurements in a gas to absorbed dose in some material.
Consider a gas in a walled enclosure irradiated by photons:

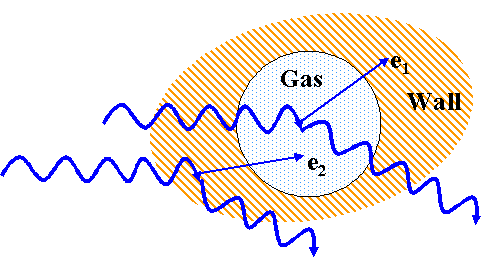
Photons interact in cavity and wall
- Chose wall material that has similar radiation absorption properties as tissue (e.g., Z)
- Cavity is very small
  - (doesn’t change angular and velocity distributions of 2⁰electrons)
- “Electronic equilibrium” exists in cavity
  - (# e^- stopping = # e^- starting in cavity)
  - requires wall thickness > range of 2^o e
Ionizations in the gas
Can measure the charge liberated.
If you know the energy required to ionize the gas,
Then the dose to the gas is:
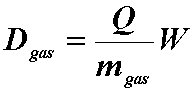
where,
- Q = coulombs of charge liberated
- W = average ionization energy for the gas
- m = kg of gas in the cavity
Example: A cavity filled with (1 cm³) air at STP is exposed to a radiation field that liberates 3.336X10^-10 C. What is the dose to the air?
At STP:
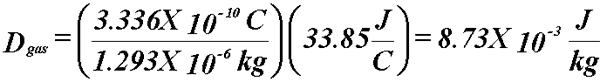
Know the dose to the gas.
- What about the dose to the medium surrounding it?
Assume our cavity is really small...small enough that it does not disrupt the electron spectrum.

Wall thickness must be as great as range as secondary charged particles (not too great to attenuate beam)
Then energy absorbed per unit mass of wall is related to that absorbed per unit mass of gas by:
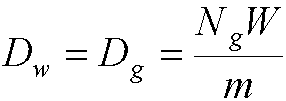
Note - this special case is where the wall and gas are the same type of material
D_w is the dose to the wall
D_g is the dose to the gas
N_q is the number of ions produced in the gas
W is eV required to produce and ion pair
m is the mass of gas in the cavity
If gas and wall don’t have same atomic composition, a slight modification is required:
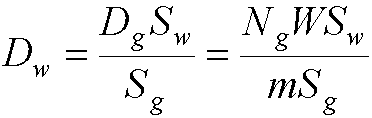
where S_g,w are the mass stopping powers of the wall and the gas
the cavity and gas pressure must be small

Example

1 cm³ of air in a block of carbon is exposed to ⁶⁰Co γ
- Q=3X10^-8 C is produced.
What is the absorbed dose to the carbon?

Mean mass stopping power ratio for ⁶⁰Co γ in carbon relative to air (Table 6.1) = 1.009

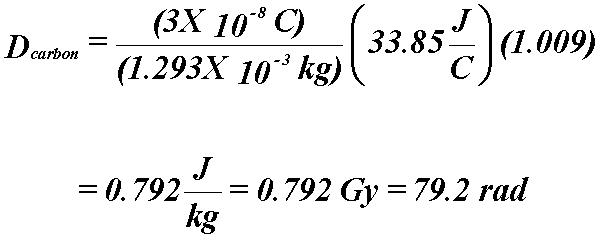
This equation allows us to measure the ionizations in a gas and relate it to dose to the medium.
If neutrons are present, the wall must be at least as thick as the maximum energy range of any secondary charged recoil nuclei produced by the nuclear interactions.
Chambers that meet these conditions can be used to measure absorbed dose to the medium