Topic 3 - Review of Fundamentals

Atomic And Nuclear Structure

Outline

• Atomic Structure
  • Rutherford’s Atom
  • Bohr’s Model
  • Modification of Bohr’s Model
  • Periodic Table
  • Characteristic X-rays
• Nuclear Structure
  • Isotopes / Nuclides
  • Binding Energy
  • Nuclear Models
  • Nuclear Stability

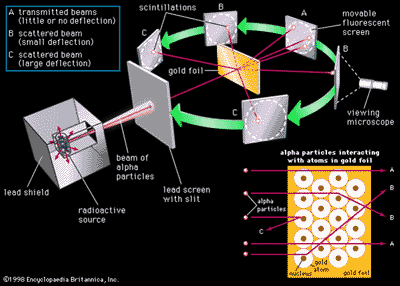
Rutherford’s Nuclear Atom

• 1911
• Postulated positive charge in center of atom, called NUCLEUS
• Hypothesis tested by Geiger and Marsden
  • Gold foil experiment
  • Alpha particles
• Experimental result
  • R = 1.2 x 10^-15A^1/3 m

Rutherford’s Atom

Gold Foil Experiment

Bohr’s Atomic Model

• Predecessor model: solar system concept
  • Issues: classical theory predicted model unstable
  • Resolution: 1913, Neils Bohr – denied validity of classical electromagnetic theory
  • New: (Max Planck) quantum theory of radiation
  • Bohr adopted Planck’s theory

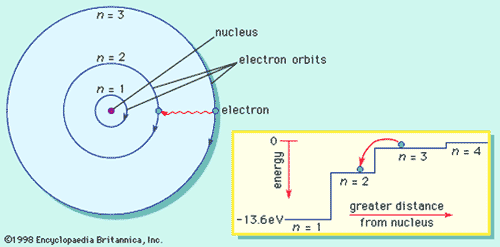
Bohr’s Model for Hydrogen

• Explained observed spectrum
• Assumed for electron:
  • travels around nucleus in a circular orbit
  • energy in an orbit is proportional to its distance from the nucleus. The further from the nucleus, the more energy it has
  • if it stays in a stationary orbit, it does not emit radiation
  • Only a limited number of orbits with certain energies are allowed (quantization of orbits using Planck's hypothesis)
  • orbits have angular momentum as integral multiple of Planck's constant divided by 2<p. 
  • can only pass from one stationary state to another.
  • Radiation is absorbed when one jumps to a higher energy orbit
  • emitted when an one falls into a lower energy orbit.
  • The energy of the radiation emitted or absorbed is exactly equal to the difference between the energies of the orbits

Bohr Atomic Model

Modification of the Bohr Atom

• Bohr theory inadequate for even H atom
  • Splitting of spectral lines
  • Sublevels of energy
  • Orbits are elliptical, not spherical, restricted by quantum conditions
  • Describing atom by 4 quantum numbers

Quantum Numbers

• A>ny of several quantities that identify the state of a physical system such as an atom, a nucleus, or a subatomic particle
• he principal quantum number for atomic electrons indicates the energy state and the probability of finding the electrons at various distances from the nucleus
  • The larger this number, the greater the energy is and the farther the electron is likely to be from the nucleus
• The four quantum number are sufficient to uniquely characterize uniquely each atomic electron

• Three quantum numbers are needed to specify each orbital in an atom
• the most important is the principal quantum number, n (the same that Bohr introduced)
• The principal quantum number specifies the energy of the electron in the orbital
• As n increases from its lowest value 1 through its allowed values 2, 3, . . . , the energies of the corresponding orbitals increase.

Principle Quantum Number

• n labels the shell of the atom.
• Each shell
  • has n² individual orbitals with the same principal quantum number
  • has orbitals that lie at approximately the same distance from the nucleus.
  • esembles the layers of an onion, with successive shells surrounding the inner shells.

Principal Quantum Number

• Hydrogen ground state
  • n = 1
  • 1 electron in the orbital closest to the nucleus.
• Ionization energy
  • energy required to elevate the electron from   n = 1 to n = ¥ 
  • energy required to remove the electron completely from the atom.

Azimuthal Quantum Number

• orbital angular momentum quantum number.
• It represents the magnitude of the orbital angular momentum of the electron around the nucleus.
• as l increases, the rate at which the electron circulates around the nucleus increases.
• The values of l in a shell of principal quantum number n are limited to the n
  values 0, 1, 2, . . . , n - 1
• the value of l in a given shell determines the subshell to which that orbital belongs.
  • n subshells in a shell of principal quantum number n.
  • 2l + 1 orbitals in a given subshell.
• conventional labels for subshells:
  • l = 0 is called an s subshell,
  • l = 1 is called a p subshell,
  • l = 2 is called a d subshell.
  • Other subshells
  • The three subshells of the shell with n = 3 are called the 3s, 3p, and 3 d

Magnetic Quantum Number

• Subshell l consists of 2 l + 1 individual orbitals.
• s subshell (l = 0) consists of a single s orbital
• p subshell (l = 1) consists of three p orbitals;
• d subshell (l = 2) consists of five d orbitals
• The individual orbitals are labeled with the magnetic quantum number, m_l, which can take the 2 l + 1 values l, l - 1, . . . , -l.

Quantum Recap

• n (principal quantum number) defines electron shells. Values are integers (n = 1,2,3,4,...).
• l (azimuthal quantum number)defines atomic orbitals. Values are integers from 0 to n-1.
• m (magnetic quantum number) defines number of orbitals of a given kind. Values are integers ranging from -l through 0 to +l.
• s (spin quantum number) has values of +½ and -½ (spin up, spin down)
  • From Pauli Exclusion Principle: no two electrons can have the same set of four quantum numbers

s orbital example

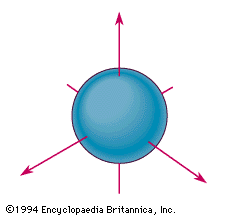
The spherical boundary surface of an s orbital. This sphere shows the region of space in which there is the highest probability of finding an electron that is described by the corresponding wavefunction

p orbitals

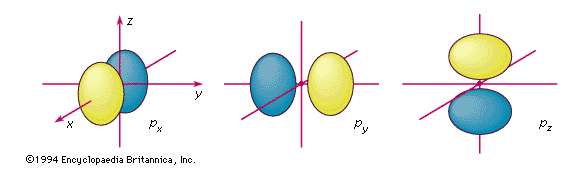
The boundary surfaces of the three p orbitals of a given shell. They are labeled according to their orientation relative to the three axes. An electron described by one of these wavefunctions will not be found at the nucleus; there is a nodal plane running through the nucleus between the two lobes.

d orbitals

The boundary surfaces of the five d orbitals of a given shell, appropriately labeled.

Periodic Table of the Elements

• Constructed with Bohr’s atomic model by application of Pauli exclusion principle

Periodic Table of the Elements

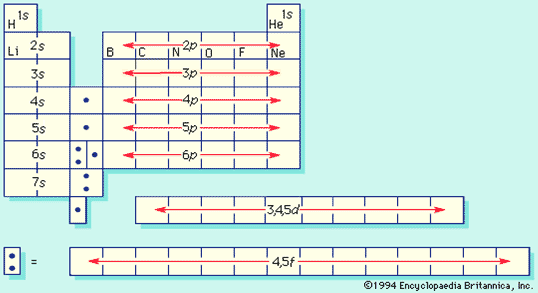
Periodic Table, again

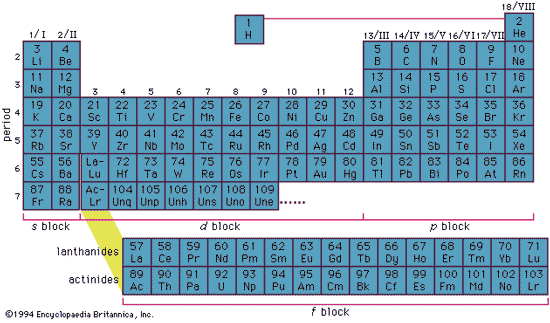
 Electronic Structure

• Inner complete electron shells constitute the core or kernel
• Binding energy of the kernel electrons is much higher than that of the valence or conduction electrons.
• Kernel electrons remain practically undisturbed in most of the processes in which the atom participates.

Consequence of Periodicity

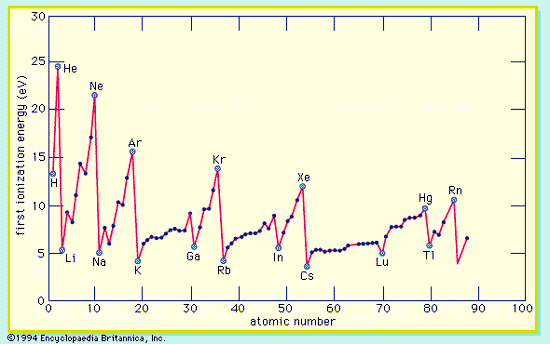
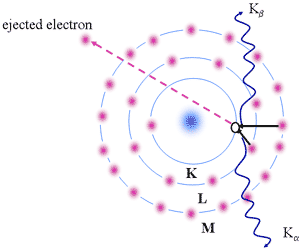
Characteristic X-rays

• Electron ejected from the kernel (e.g, K shell)
  • States with n=1,2,3,4 constitute the K,L,M,M,.. shells
• Empty state (or hole) is left in K-shell
• Another electron in a higher energy level can fall into the vacant state
• Radiation emitted by electron "falling" into  vacant state is in the X-ray spectral region  
• Electron from:   L,M,N,... valence shells
• Series of X-ray lines may be produced designated as a, b   etc.

Atomic Shell Terminology

• Optical Spectroscopists use n = 1, 2, 3, ..
• X-ray spectroscopists use K, L, M, N, O . .
• When an electron is removed from a particular shell,
  • electrons from all the higher-energy shells fill that vacancy
  • result in a series that appears inverted as compared with the hydrogen series.
  • Different angular momentum states for a given shell cause energy sublevels within each shell;
  • these subshells are labeled by Roman numerals according to their energies.

Origin of Characteristic X-rays

The Nucleus

• Terminology
• Binding Energies
• Nuclear Models

Isotopes and Nuclides

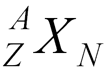
• A is atomic mass number (protons + neutrons)
• Z is atomic number (protons)
• N is neutron number
• X is chemical symbol

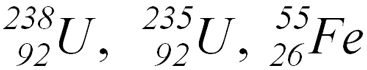
• Isotopes (U)
• Nuclides (U, Fe)

Binding Energy

Hypothetical energy released if a nuclide were synthesized from Z separate H atoms and N (equal to A - Z) separate neutrons.

Average binding energy per nucleon shows a maximum at ⁵⁶Fe falling off gradually on both sides to about 7 MeV at ⁴He and to about 7.4 MeV for the most massive nuclei known.

Most of the naturally occurring nuclei are not stable in an absolute nuclear sense.

Mass defect

• W = Z_m(H) + (A-Z)_m(N)
  • weight of sum of parts > actual weight
  • mass defect
• d = W – M
  • represents mass equivalent of work done to separate nucleus into components,
  • in energy units, called Binding energy (BE)
• BE= (W – M)amu x 931 MeV/amu
• E_b = 931(W-M)/A; MeV/nucleon

Binding Energy per Nucleon

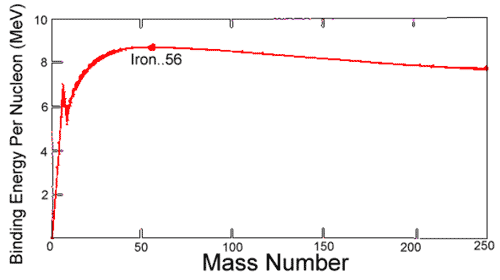
Binding Energy

• Nuclei heavier than iron gain energy by degrading into products closer to iron
  • Only for heavy elements does alpha decay and spontaneous fission attain observable rates.
• Nuclear energy is gained by fusion of most elements lighter than iron
  • coulombic repulsion keeps fusion rates low
  • exception: if nuclei are subjected to greater than 10⁷ K in hot cores of stars, thermonuclear bombs, controlled fusion plasmas

Nuclear Models

• Building blocks known (n, p, subatomics)
• No definite structure defined
• Analogous to atomic system
• Three major models:
  • Liquid drop
  • Shell model
  • Combined model

Liquid Drop Model

Formulated (1936) by Niels Bohr and used (1939) by him and John A. Wheeler to explain nuclear fission.

Nucleons (neutrons and protons) behave like the molecules in a drop of liquid.

If given sufficient extra energy (as by the absorption of a neutron), the spherical nucleus may be distorted into a dumbbell shape and then split at the neck into two nearly equal fragments, releasing energy.

Liquid Drop Model– Bohr & Wheeler

Although inadequate to explain all nuclear phenomena, provides excellent estimates of average properties of nuclei

Key points:

• Nucleus homogenous mixture of nucleons
• Internal energy equally distributed
• Surface tension keeps nucleus spherical
• Explains nuclear fission
• Allows calculation of atomic masses
• Nuclear binding energy can be understood with the model of a charged liquid drop.

Shell Nuclear Model

• Description of nuclei similar to Bohr atomic model of electron energy levels.
• Developed by the American physicist Robert Hofstadter in the 1950s.
• Constituent nuclear particles are paired
  • neutron with neutron and proton with proton
  • magic numbers: filled nuclear-energy levels when the number of protons or neutrons equals 2, 8, 20, 28, 50, 82, or 126indicate especially stable nuclei.
  • The unpaired neutrons and protons account for the properties of a particular species of nucleus as valence electrons account for the chemical properties of the various elements.
  • The shell model accurately predicts certain properties of normal nuclei, such as their angular momentum;

Collective model

• Also called UNIFIED MODEL, Incorporates aspects of both the shell model and the liquid-drop model Explains certain magnetic and electric properties that neither of the two separately can explain:
• High-energy states of the nucleus
• certain magnetic and electric properties (magnetic and quadrupole moments)
• explained by the motion of the nucleons outside the closed shells combined with the motion of the paired nucleons in the core.
• Nuclear core
  • thought of as a liquid drop on whose surface circulates a stable tidal bulge directed toward the rotating unpaired nucleons outside the bulge.
  • Tide of protons (positively charged particles) constitutes a current that in turn contributes to the magnetic properties of the nucleus,
  • the greater deformation of the nucleus as the number of unpaired nucleons increases accounts for the measured electric quadrupole moment (an index of nuclear shape -  a measure of how much the charge in space departs from spherical symmetry).

Nuclear Decay Schemes

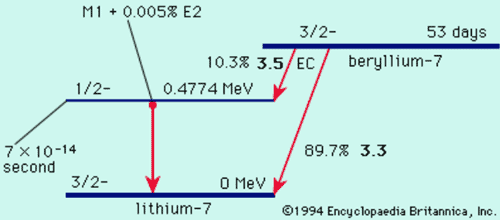
Nuclear Stability

• Binding energies
• Proton vs neutron number
• Table of isotopes

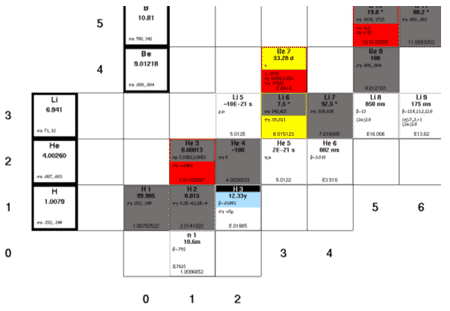
Chart of the Nuclides

Nuclear binding energies, shown as a function of atomic mass number

Nuclear Stability Curve