|
|
|
 |
|
| Welcome | Contact | Getting Started | Site Map | Project | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Topic 3 - Review of Fundamentals
Radioactivity |
Outline
- Radioactivity and transformation mechanisms
- Transformation kinetics
- Activity
- Naturally Occurring Radioactivity
- Serial Transformations
Radioactivity
- Spontaneous decay (disintegration) of the NUCLEUS of an atom
- Involves energy changes in the NUCLEUS
- Results in:
- particle + KE
- energy
Band of Stability
- The Band of Stability
- There is no known formula to predict if an isotope will be stable.
- Example 56Fe has highest binding energy per nucleon
- 53Fehas a half-life of t½ = 8.5 minutes
- 60Fet½ = 300,000 years
Nuclear Stability Curve
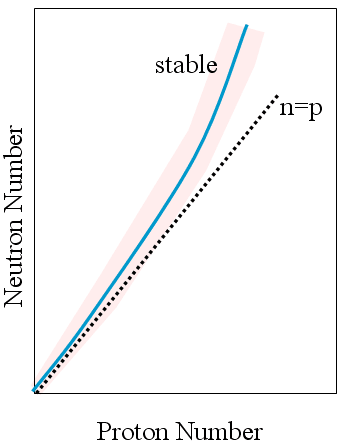
- Rule
of thumb for predicting stability
- Plot all known isotopes (t½ > 10-8 s) as no vs p+
- two lines can be drawn to enclose all of the stable nuclei
- Between these 2 lines lies the Band of Stability
- no/p+ ratio increases as atomic number increases.
- As more protons packed into nucleus, larger numbers of neutrons required to compensate strong force - to "dilute" the proton-proton electrostatic repulsions.
- Isotopes above and to the left tend to ß -emitters.
- Isotopes below and to the right tend to be positron emitters.
- Isotopes above atomic #83 tend to be a emitters.
Stability Quirks – Odd Even Rule
- If n’s and p’s are both even, isotope is likely stable
- Of
264 known stable isotopes
- only 5 have both odd numbers
- 157 have both even numbers
- 102 have both an odd and an even number.
- The
odd-even rule is related to the spins on the nucleons:
- Both p+ and no have spins. When two like particles have paired spins, combined energy is less than when their spins are not paired.
- When even numbers of p+ and no all the spins can be paired and the system has less energy (i.e. more stable) then when an odd proton or odd neutron is present.
Stability Quirks – Magic Numbers
- Isotopes
with specific numbers of protons and neutrons are more stable then the
rest.
- Numbers are 2, 8, 20, 28 , 50, 82, and 126.
- When both the numbers of the p+ and the number of no are the same magic number the isotope can be quite stable.
- eg. 42He, 168O, 4020Ca
- All these isotopes are extremely stable.
- 20882Pb has 82 p + and 126 no
- Existence of magic numbers supports the hypothesis that there are nuclear energy levels similar to electron energy levels.
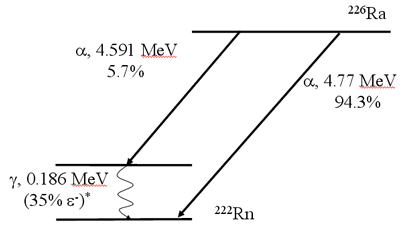
Alpha Decay
- Occurs in heavier elements (BE curve)
- Proton rich
- Discrete energies
- Great way for the atom to lose a lot of energy at one time
Alpha Decay
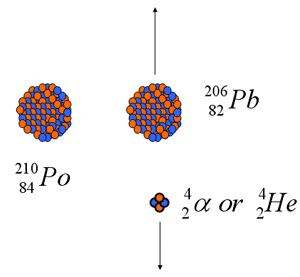
- 210Polunium is one example
- Reaction equation:
- Atomic numbers conserved in decay
- With one exception (147Sm) naturally occurring alpha emitters found Z>82
- Reason
- look at n/p ratio
- electrostatic repulsive forces increase more than cohesive nuclear forces
- emitted particle must have sufficient energy to escape potential barrier
Potential Energy Near the Nucleus
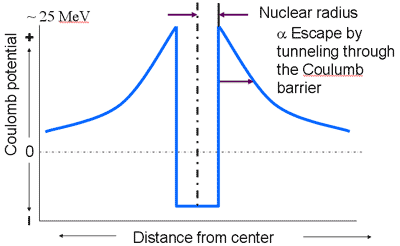
Energetics for Alpha Emission
- Mp = Md + M a + 2Me + Q
- Q
= total energy release of transformation
- no gamma,
- energy divided between alpha and progeny (causes recoil, or “creep”)
- energy allocation dictated by conservation of energy and momentum
- Q
= ½MV2 + ½mv2
- but MV=mv (conservation of momentum),
- if E= ½mv2 then E= Q/(1+m/M)
Decay Scheme (Alpha Emission)
Alpha Radiation

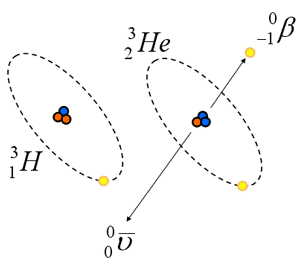
Beta Emission (b-)
- Electron that is ejected from nucleus
- Single negative charge (1.6 x 10 -19C)
- Small mass (0.00055 amu)
- “formed at instant of emission ” by transformation of neutron into a proton and electron:
- surplus of neutrons required
- Mp= Md + Me* + Q
Beta Decay
- Emission of an electron (a.k.a. negative electron, negatron, Beta)
- Reaction Equation:
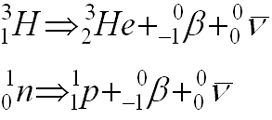
Beta Decay
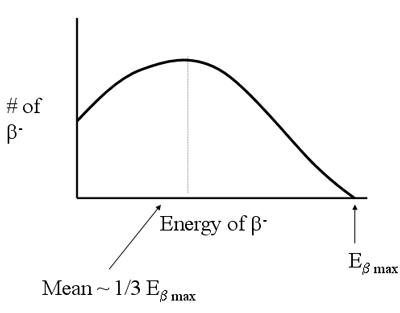
- Continuous energy distribution
- Anti-neutrino shares KE
- Also have a short range (~mm in H2O)
- Distribution of energies
- nternal and limited external concern
Decay Scheme (Beta Emission)*
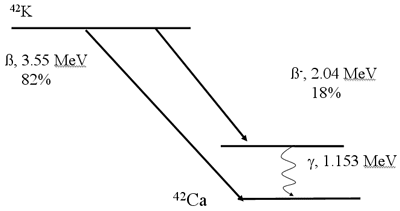
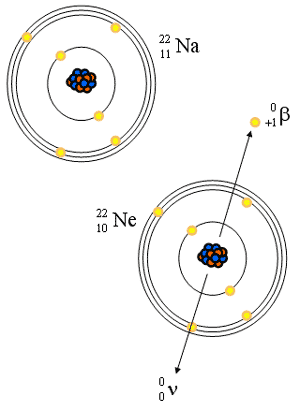
Positron Decay
- Too few neutrons for stability
- Emission of a positron
- Net effect: gain n, lose p
- Positron is an electron with a positive charge (Star Trek anti-matter)
- Reaction equations:
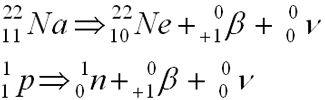
Positron Decay
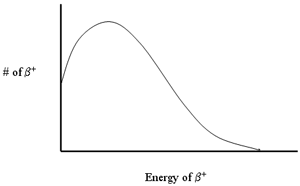
- Distribution of energies
- Annihilation gamma rays
Decay Scheme (Positron Emission)

Orbital Electron Capture
- Positron emission requires mass difference between parent and progeny equal to two electron masses
- If not, then extranuclear electron (K shell) can be captured with same result
- Mp +Me = Md + f + Q
![]()
- neutrino in this case is monoenergetic
Orbital Electron (K) Capture
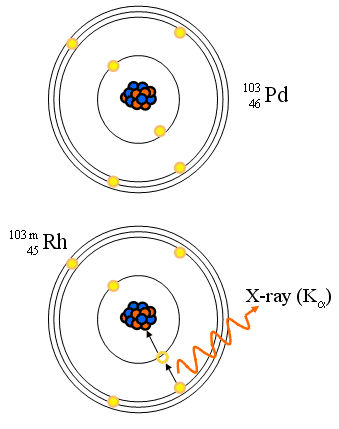
- Orbital electron is absorbed within the nucleus
- Characteristic X-rays
- Reaction equation:
![]()
Gamma Ray (Isomeric Transition)
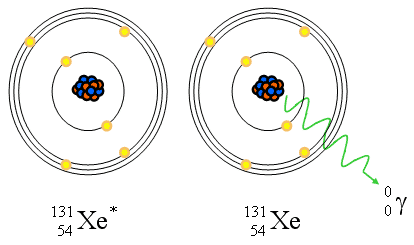
- Gamma ray emission
- Isometric because Z and A do not change
- Pure energy release from a “excited state” nucleus
- Reaction equation:
![]()
Isomeric Transition
- Usually seen from daughter (progeny)
- Discrete energies!
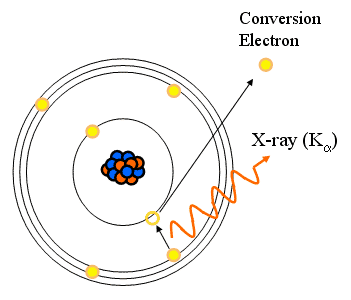
Internal Conversion
- Alternative to gamma emission
- There is a small probability that an orbital electron can pass within the nucleus
- Energy is transferred to the electron and immediately ejected from the nucleus
- Reaction equation:
![]()
- It is said to “compete” with isomeric transition
- Characteristic X-rays
- Discrete energies!
- Eg = Ee + f
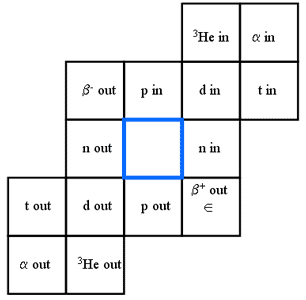
Chart of the Nuclides
TRANSFORMATION KINETICS
- Half-life
- Average Life
- Activity
- Specific Activity
Half-life
- The time required to reduce the activity to half its initial value
- Decreases exponentially
Relationship Between Half-life and Activity
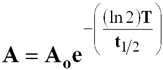
- A = activity
- Ao = initial activity
- e = Euler ’s Constant
- (2.71…..)
- T = Time
- t1/2 = half-life
The Decay Equation
The activity of a nuclide decreases with time. Let N be the number of radioactive atoms in the sample at any particular time. The change in the number of atoms over a short time is dN and the time period is dT. The rate of change is proportional to both the number of atoms and to dT. This constant of proportionality is called lambda (?), the decay constant. This can be written:
dN = - l N dt
Notice that the negative sign means the number of atoms is decreasing with time.
The Decay Equation
The units for the variables in this equation are:
N = atoms
dN =
change in atoms over a short time
dt =
a short period of time (s)
l = per time
(s-1)
The decay rate [A(t)], called
activity, is given by:
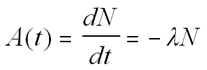
The Decay Equation
How do you predict the activity (or the number of atoms
left) at some time later? Let us
start with our first differential equation:
dN =
- l N dt
Now separate the variables and rearrange:
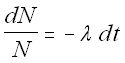
The Decay Equation
Now you can integrate this equation:

The solution to this is:
![]()
The Decay Equation
If we specify that N0 atoms are present at the time t = 0, then resubstitution into the equation above gives:

The Decay Equation
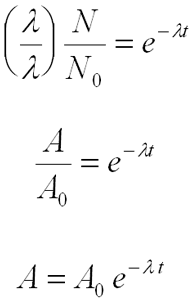
Determining Half-life
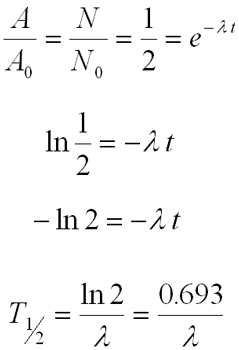
Activity & Specific Activity
- Activity(A)
- Becquerel
- 1Bq = 1 disintegration / second (dps)
- Curie
- 1Ci = 3.7X1010 dps
- based on activity (decay rate) of 1 g of 226Ra
- Becquerel
- Specific
Activity (SA or SpA)
- Activity per mass
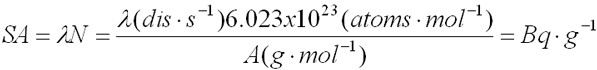
|
|
| Welcome | Contact | Getting Started | Site Map | Project | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |