|
|
|
 |
|
| Welcome | Contact | Getting Started | Site Map | Project | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Topic 3 - Review of Fundamentals
Interactions of Radiation With Matter |
Outline
- Beta Radiation
- Range-energy relationship
- Mechanisms of Energy Loss
- Alpha Rays
- Range-Energy Relationship
- Energy Transfer
- Gamma Rays
- Exponential Absorption
- Interaction Mechanisms
- Neutrons
- Production/Classification/Interaction
Beta Rays (Particles)
Range-Energy Relationship

Curve of 210Bi 1.17 MeV beta particles with Al absorbers
Determination of range
- End point in absorption curve = range
- Rule of thumb:
- Absorber half-thickness = 1/8 range of beta
- Systematic experiments have established beta range as function of material, energy:
Range-energy Curve for Beta Rays in Various Substances
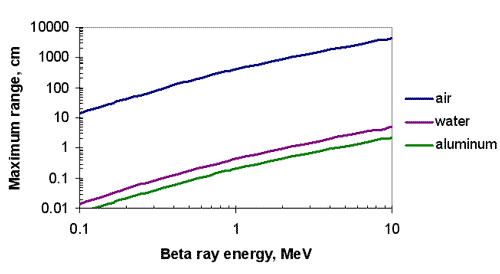
Range-Energy Observations
- Required absorber thickness increases with increasing energy (!!)
- Range is largely a function of electron density ( per cm2),
- To a lesser degree range is a function of Z
- Result has practical implications for shielding
- Atomic number neglected
- Areal density is used
Density thickness
- Areal density of electrons
- Proportional to product of absorber density and linear thickness:

*Units can differ from those shown, as long as they are internally consistent
Advantage of density thickness
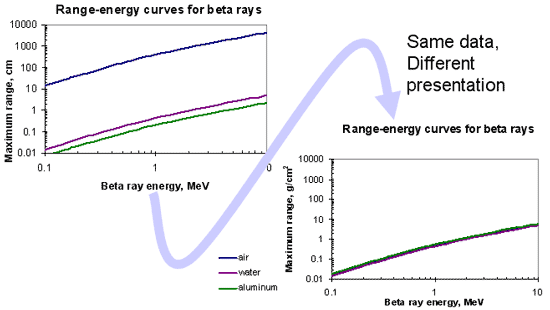
Range Energy Curve for Beta Particles
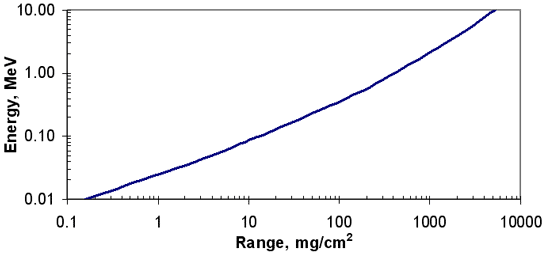
Beta Range – Empirical Equations
- R = 412E1.265 – 0.0954 ln E
- for 0.01
 E
E
 2.5 MeV
2.5 MeV
- for 0.01
- ln E = 6.63 – 3.2376 (10.2146 – ln R)1/2
- for R
 1200
1200
- for R
- R = 530 E – 106
- for E > 2.5 MeV, R > 1200
- where
- R = range, mg/cm2
- E = maximum beta-ray energy, MeV
Beta Particles – Energy Loss Mechanisms
Ionization and Excitation
- Interaction between electric fields of beta and orbital electrons
- inelastic collisions
- energy loss by beta f(distance, KE)
- Ek = Et - f
- Ek = kinetic energy of ejected electron
- Et = energy lost by beta particle
- f ionization potential of absorbing medium
- Ejected electron may produce additional ion pairs (clusters, delta rays)
Ionization Potential vs Energy Expended
Average energy lost by a beta particle in the production of an ion pair
Gas
|
Ionization
Potential, eV |
w, Mean energy expended per ion
Pair, eV
|
H2
|
13.6
|
36.6
|
He
|
24.5
|
41.5
|
N2
|
14.5
|
34.6
|
Air
|
---
|
33.7
|
CH4
|
14.5
|
25.7
|
C2H4
|
12.2
|
26.3
|
Difference is attributed to electronic excitation
Linear Rate of Energy Loss by Beta Particle
- Called specific ionization
- Ionization
- Excitation
- Key
- Understanding biological impacts
- Detector design and response
- Number of ion-pairs formed per unit distance traveled.
Specific Ionization

Relationship of beta particle energy to specific ionization of air
Specific Ionization (S.I.)
- Number of ion-pairs created per specific distance traveled by the beta particle
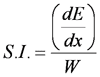
- Where
- dE/dx is the energy loss due to ionization and excitation per cm traveled (eV/cm)
- W is the mean energy (eV) required to create an ion pair;
- High values for low-energy betas
- Decreases rapidly as beta energy increases
- Broad minimum around 1 MeV,
- Slowly increases at energies above this point
Specific Ionization - Beta Energy Loss, MeV/cm
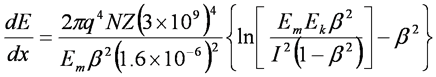
- Where
- q = charge on one electron
- N = number of absorber atoms per cm3
- Z = atomic number of the absorber
- NZ = # of absorber electrons per cm3
- Em = energy equivalent of electron mass (0.511 MeV)
- Ek = kinetic energy of the beta particle, MeV
- b = v/c = speed of particle relative to c (light)
- I = mean ionization and excitation potential of absorbing atoms, MeV
Mean Excitation Energies (I)
- Calculated for several elements from quantum principles
- Measured
- Approximate empirical formula:
- I ~ 19.0 eV for Z = 1
- I ~ 11.2 +11.7Z eV for 2 <=Z <= 13
- I ~ 52.8 +8.71Z eV for Z > 13
Mass Stopping Power
- Another way to express energy loss
- If density thickness is used instead of length, then:

- Where S is the Mass Stopping Power ,
- r is the density of the absorber
Linear Energy Transfer
- Specific Ionization used to describe energy lost by the radiation
- In radiobiology, focus is on linear rate of energy absorption in the medium.
- This measure is Linear Energy Transfer

- dEl is the average energy locally imparted to absorbing medium by particle traversing dl
- "Locally Imparted" refers to either
- maximum distance from the track of the particle, or
- maximum value of discrete energy loss
- Either case, LET refers to energy imparted within a limited volume of absorber
Energy Transferred vs Absorbed
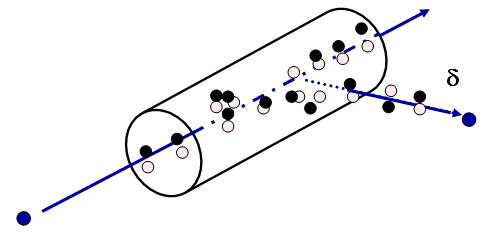
- The initial b-(blue) is losing energy by creation of ion pairs or delta rays. Not all its lost energy is localized.
- LET is energy deposited within the volume shown by the cylinder
Relative Mass Stopping Power
- Compares energy absorptive power of different media.
- Defined as:
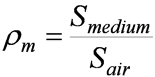
- rm is not a density
- Is relevant to dose measurements……
Bremsstrahlung
- X-rays emitted when high-speed charged particles are rapidly accelerated
- b passes close to nucleus and is deflected from path
- Heavy nuclei are more effective in causing deflections
- Single electron can emit X-ray up to its own kinetic energy
- Monoergetic beam of electrons produces a continuous spectrum
Estimating Bremsstrahlung Production
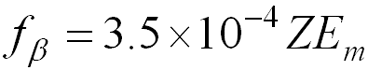
- f b is the fraction of incident beta energy converted into photons (Bremmstrahlung)
- Z = atomic number of the absorber
- Em = maximum energy of the beta particle
Importance of Bremsstrahlung
- b particles can excite and ionize atoms
- Also radiate energy via bremsstrahlung
- Relative contribution important only at high energies
- high energy photons can be created
- additional shielding problem from high-energy beta emitters
Stopping Power Stopping Power for Electrons in water in MeV cm2/g
Radiative to Collisional Losses

X-ray Production from Monoenergetic Electrons
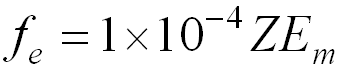
- fe is the fraction of energy in electron beam converted into X –rays
- Z = atomic number of the absorber
- Em = maximum energy of the beta particle
ALPHA RAYS (PARTICLES)
Alpha Particles
- Least penetrating of radiations
- in air, range ~ few cm
- in tissue, ~ microns (10-4cm)
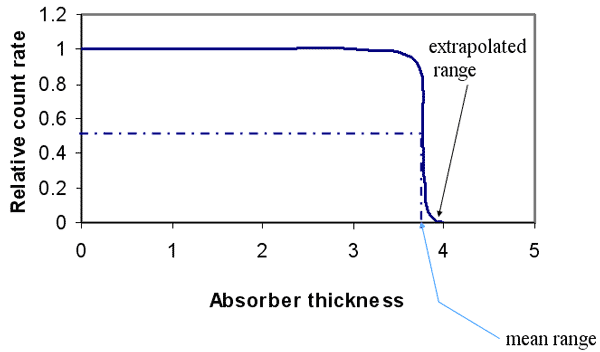
- Range
- mean range
- extrapolated range
Alpha-particle Absorption Curve
Alpha Particles – Range
- Empirical equations for Alphas in air
- R = 0.56 E
- R in cm
- E in MeV, E< 4 MeV
- R = 1.24 E –2. 62
- R in cm
- E in MeV, 4 <E< 8 MeV
- For range in air at 00 C and 760 mm pressure
- Empirical equations for Alphas in other media
- Rm = 0.56A1/3R
- Rm is in mg/cm2
- A = atomic mass number of the medium
- R = range of the alpha particle in air, cm
Alpha Particles, Energy Loss
- Only significant mechanism:
- interaction with electrons in absorbing medium
- at very slow speeds nuclear collisions can occur
- only small energy transfers occur at each interaction
- Result in excitation and ionization of absorber atoms
- On average, alpha loses 35 eV per ion pair
- Because of high charge and low velocity
- (due to mass) specific ionization is very high
- path is almost straight
- energy loss is essentially continuous
Comparison with e-,+
- Electrons and positrons
- lose energy almost continuously as they slow
- can lose large fraction of energy in single collision with atomic electron (equal mass)
- large deflections
- frequently scattered through large angle deflections by nuclei (result: bremsstrahlung)
- HCPs
- straight line paths
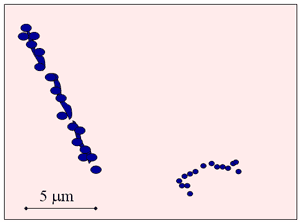
Alpha- vs Beta –particle tracks
Alpha Particle Bragg Peak

Alpha Particles, Energy Loss
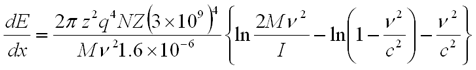
- Where
- Z = atomic number of ionizing particle
- q = unit electrical charge. 1.6 x 10-19C
- zq = electrical charge on the ionizing particle
- M = rest mass of the ionizing particle, gms
- V = velocity of the ionizing particle, cm/s
- N = number of absorber atoms per cm3
- Z = atomic number of the absorber
- NZ = # of absorber electrons per cm3
- C= velocity of light, 3 x 1010cm/s
- I = mean ionization and excitation potential of absorbing atoms, for air= 1.38 x 10 -10erg
Notes re energy transfer equation
- Previous equation appropriate for other heavy charged particles (HCPs)
- derived by Bethe from quantum mechanics
- various versions around
- logarithmic term leads to increase in stopping power at energies
- low energies, lhs of equation dominates
- Bragg peak consequence of ln term decreasing
GAMMA RAYS
Gamma Rays
- Key differences in charged and uncharged particle interactions
- photon electrically neutral
- does not steadily lose energy as it penetrates
- interaction is statistically governed by:
- medium
- photon energy
- probability described by coefficient
Photon Interactions
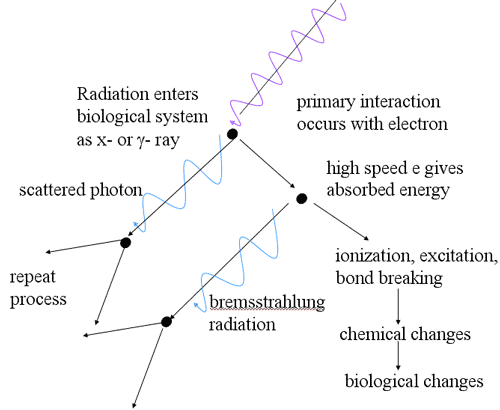
Nature of Photon Interactions
- Absorption with disappearance of photon
- Scatter
- direction change
- energy change
- no energy change
- Principal methods of energy deposition
- photoelectric
- Compton scattering
- pair production
- photonuclear reactions
Describing Photon Behavior
- Exponential Absorption Equation
I = I0e-mt
- I0_ = photon intensity with no absorbers
- I = photons transmitted through absorber
- t = absorber thickness
- e = base of natural logarithm (~2.71828183…)
- m = atteunation coeffcient (slope of absorption curve)
Determining Attenuation Coefficients
- Measurements taken under conditions of good geometry
- monoenergetic
- well-collimated
- narrow beam
- Data plotted as semi-log
- straight line
- slope is m
- intercept is I0
Good Geometry Conditions
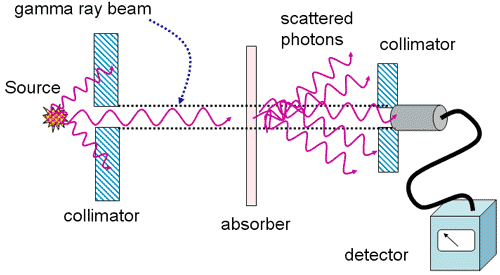
Attenuation of 137Cs Gamma Rays under conditions of good geometry
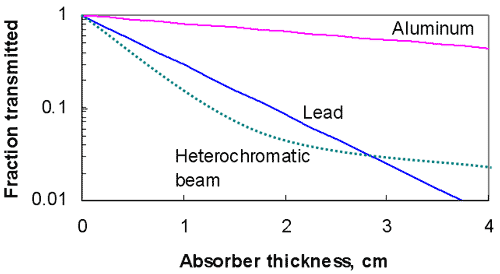
Additional Considerations
- e-mt
- Exponential term – must be dimensionless,
- m and t must have reciprocal dimensions
- m or ml
- Linear attenuation coefficient
- Total attenuation coefficient
- m/r (mass attenuation coefficient)
- also identified as mm
- units g/cm2
- paired with t expressed as density thickness
- Atomic attenuation coefficient, ma
- ma = ml / N
- ma = ml / N
Linear, Mass, Electronic, and Atomic Attenuation Coefficients
r is the density; Ne is the number of electrons per g; Z = atomic number of the material
Miscellaneous Relationships
- Number of atoms per g = NA/A
- NA = atoms per mol
- A = gms per mol
- Number of electrons per g = NAZ/A = Ne
- Number of electrons per kg= 1000 Ne
Photon Interaction Mechanisms
- Photoelectric effect
- Scattering
- Pair (and triplet) production
- These 3 mechanisms result in electron emission from material interacting with the photon
- Photonuclear reactions
- This mechanism initiates a nuclear reaction and results in emission of other radiations
Summary of Photoelectric Effect
- Involves bound electrons
- Probability of ejection is greatest if photon has just enough energy to knock electron from shell
- Cross section varies with photon energy, approximately 1/hn3
Interaction Mechanism - Photoelectric Effect
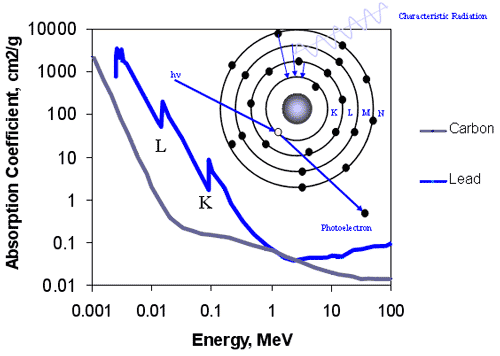
Compton Scattering
- Elastic collision between photon & “free” e
- photon transfers some, not all, of its energy
- Scattered photon, and e, result
Probability of Compton interaction
- Decreases with increasing Z
- For low-Z elements, Compton interaction predominates
- every electron acts as a scattering center
- electron density is important
- scatter described wrt solid angle
- Klein-Nishina equation describes scattering coefficient
Compton relationships
- Energy of scattered photon
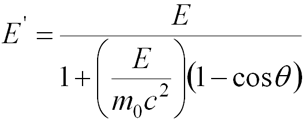
Klein-Nishina
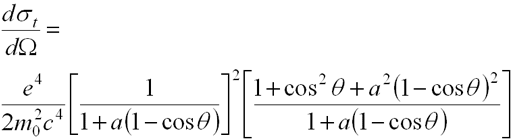
- Scattering into differential solid angle dW at angle q
- a defined as
- hn/m0c2
- or hn (expressed in MeV)/0.511
Summary for Pair Production
- Interaction between photon and nucleus
- Threshold is 1.02 MeV
- Increases rapidly above threshold
- Coefficient
- per atom varies ~Z2
- per mass Z1
- Energy transferred to KEparticle = hn-1.022
- 2 annihilation photons, each 0.511 MeV
Photonuclear Reactions
- Photodisintegration
- Nucleus captures photon, typically emits a neutron
- Generally requires high energy photons
- ~ 6 to 8 MeV common
- Exception: 9Be(γ,n)8Be - threshold is 1.666 MeV
- Significant for electron accelerators
- Betatrons
- Synchrotrons
- Linear accelerators (common in hospitals)
Summary of Photon Interactions
Photon Interactions: Combined Effects
- Attenuation coefficients are probabilities of removal of photons
under good geometry considerations.
- Total attenuation is sum of interaction mechanisms. Principal
components are:
mt= mpe + mcs + mpp
where each has its own probability based on energy and absorbing material – does not account for fraction carried away via annihilation - mt gives fraction of energy of a beam removed per unit distance traveled in absorber
- Total attenuation is sum of interaction mechanisms. Principal
components are:
Photon Interactions: Combined Effects
- Absorption coefficients considers only the fraction of beam energy
that is transferred to the absorber by:
- Photoelectron
- Compton electron
- Electron pair (from pair production)
- Doesn’t consider
- Scattered compton photon
- Annihilation radiation after pair production
- Absorption coefficients:
- e= mpe + mcs + mpp(hn -1.02)/ hn
Relative Importance of Reactions
Energy Transfer and Energy Absorption
- Photon interaction with absorber complex
- scattered photon
- kinetic energy of electron
- collisional losses
- brehmsstrahlung radiation
- Calculate
- Etr average energy transferred
- Eab average energy absorbed
- difference is bremsstrahlung
Summary
- Energy transfer from radiation field to absorbing medium is basis of radiation effects
- Charged particles
- excite or ionize atoms
- Have definite range in matter
- exhibit Bragg peak
- Photon (x, gamma) differ qualitatively
- indierctly ionizing
- interact with atomic electrons (pe, scatter, pp)
- stochastic events
NEUTRONS
Neutrons
- No ‘natural’ neutron emitters
- Sources of neutrons
- Fission (reactors)
- Pu
- U
- Spontaneous nuclear fission:
- 252Cf
- Photoneutron sources
- Other forms of nuclear bombardment
- Fission (reactors)
Fission
- 235U, 233U, Pu
- Neutron absorbed by fissionable nucleus
- Nucleus becomes ‘compound nucleus’
- Nucleus may then fission, or decay by other emission
235Cf
- Emits alphas
- Also spontaneously fissions
- Neutrons emitted with fission
- 10 fissions per 313 alpha emissions
- Most probable neutron energy is 1 MeV
- Average neutron energy is 2.3 MeV
- Half life (T1/2,sf) = 2.65 years
- (both decay modes)
- T1/2,a= 2.73 y
- What is T1/2,sf?
Photoneutrons
- Photodisintegration
- photons break up nucleus
- protons, neutrons, and deuterons (a proton and neutron bound together) are ejected.
- Photoneutrons:
- Photon incident on nucleus contains enough energy to overcome binding energy of nucleons
- Neutron is emitted
- Photons (gamma rays) are monoenergetic
- Neutrons are monoenergetic
- Low binding energy target atoms used (Be)
- See Table 5.4 on page 151
Table 5.4 a,n Photoneutron Sources
Other Neutron Production Methods
- (a, n) : An alpha particle is absorbed by a 9Be nucelues
- 9Be + 4He --> (13C)* --> 12C + 1n
- Neutrons are poly energetic
- Alphas lose energy prior to reaching 9Be
- Typically alpha emitter mixed in powder form with alpha source
Table 5.5 a,n Neutron Sources
Other Neutron Production Methods
- Accelerators may also be source of alphas
- Table 5.5 on page 152 has a list of typical a, n sources
- Typically favored over photoneutron sources since they have a significantly longer half life
- Note that all neutrons are born ‘fast’
- What is a ‘fast’ neutron?
Classification
- Neutrons are classified according to their energy
- Neutron reactions are very dependant on energy
- Only two classifications important at this point
- Fast neutrons
- Generally greater than 0.1 MeV
- Thermal
- Have same KE as gas molecules in their environment:
- Fast neutrons
Maxwell-Boltzmann Energy Distribution - As Function of Temperature
Thermal Neutrons
- Also called ‘slow’ neutrons
- Defined more precisely than fast or other types of neutrons:
- At 293°K
- 0.025 eV most probable energy
- 2200 m/s most probable velocity
- At 293°K
Maxwell-Boltzmann distribution - gas molecules
Thermal Neutrons
- Calculating most probable energy
- Equation 5.40
- Emp= kT
- Average Energy:
- Equation 5.41
- E = 3/2 kT
- Can E = 1/2 mv2 be used for neutrons?
- Gives velocity of thermal neutrons
Neutron Interaction
- All neutrons are born fast
- Lose energy by collisions with nuclei
- Inelastic
- Elastic
- Collisions of fast neutrons are typically elastic
- With low Z absorbers
- "billiard ball" type of collision
- KE and momentum conserved
- Low probability for capture
- Thermal neutron collisions may result in elastic collisions or capture
- Elastic scattering and capture are most important for HP
- Capture of a neutron is typically followed by emission of a photon or other particle from nucleus
- Neutrons are removed exponentially when a material is placed in a neutron beam
Absorption
- Linear or mass attenuation coefficients are not typically used with neutrons
- Microscopic cross section or macroscopic cross sections are normally given for a material
- Microscopic cross section = s = cm2 / atom
- Macroscopic cross section = S = s N = cm-1
Cross Sections
- Absorption cross section may include activation cross section
- Absorption cross section does not include scattering cross section
- Total cross section is the sum of all cross sections, including scattering, activation and other reactions
- All cross sections are VERY energy dependent
- Typically, only thermal neutron cross sections are listed
- Be very careful in using cross sections; Tables are not always clear on how to use them properly
- Absorption cross sections are said to be about 1/3 of the total cross section, but this is only a rough estimate
Removal of Neutrons
- Equation 5.43 is used with the absorption cross section to find neutron removal from a beam of neutrons
- I = I0e-sNt
- I0 = initial neutron intensity
- I = final neutron intensity
- N = number atoms absorber per cm3
- t = thickness of material in cm
- s = microscopic cross section for absorption in cm2/atom
- Note that if more than one method for removal is possible, it should be included in the cross section
- Equation 5.43 can also be used to find activation quantities
1/v Law
- Although cross sections are temperature dependant, can ‘correct’ cross sections for 0.001 to 1000 eV
- Use Equation 5.53 to find cross sections at different energies
- Note that there are some atoms that do not follow the 1/v law
- Called ‘not 1/v’ atoms
- Simply multiply by a factor to obtain the desired result
- Compilation of ‘not’ 1/v atoms in “Introduction to Nuclear Engineering” by John Lamarsh, 2nd Ed. p. 63
Cross Section Notes
- The cross sections used in calculations should be for poly energetic neutrons if reactor or (a, n) reaction
- Tables normally list cross sections for mono-energetic thermal neutrons
- Beware of extrapolating outside limits of 1/v (> 1000 eV)
- Beware of resonances and competing reactions
- Divide cross section by 1.128 to correct a monoenergetic neutron
beam cross section to a poly energetic beam cross section
- More detail on this in Chapter 12 later
- BNL is generally best source for cross sections
Neutron Absorption
- Neutron absorption may result in:
- Formation of a stable isotope of an atom and emission of a photon
- Fission
- Emission of an alpha particle
- Activation of an atom
- Other, more exotic reactions
Activation
- When neutron absorption leads to too many neutrons
- Neutron is absorbed
- Gamma emitted (prompt)
- Atom is now radioactive
- Typically beta (negatron) emitter
- Sometimes alpha emitters formed
Activation
- Equation 5.58
- lN = fsn (1 - e-lt)
- lN = Activity in Bq
- f = Flux, neutrons per cm2 per sec
- s = Activation cross section, cm2
- n = Number target atoms
- t = Time of irradiation
- l = Decay constant, induced activity
Scattering
- Energy lost best through collisions with atoms of same mass as neutron
- "Billiard ball collisions"
- Scattering with ‘heavy’ atoms typically does not result in much energy loss
- Measure of energy loss = average logarithmic energy decrement per collision (See p. 155)
Neutron Energy Loss
- Scattering is how a neutron becomes thermal
- Hydrogen has the highest average logarithmic energy decrement per collision (almost same mass as neutron)
- Median amount of energy transferred from neutron to hydrogen in one collision is 63%
Neutron Life
- Fast Diffusion Length - average linear distance a fast neutron travels
- Thermal Diffusion length - average linear distance a thermal neutron travels
- Note that actual neutron paths are very tortuous
- Diffusion lengths are only of concern when absorption cross section is small
- Typically measured, many assumptions required for calculations
Summary
- Neutrons slowed down by scattering with light nuclei
- Absorption of neutrons more likely with thermal neutrons
- Activation is possible when neutron absorption occurs
- Exercise caution when using cross sections
|
|
| Welcome | Contact | Getting Started | Site Map | Project | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
